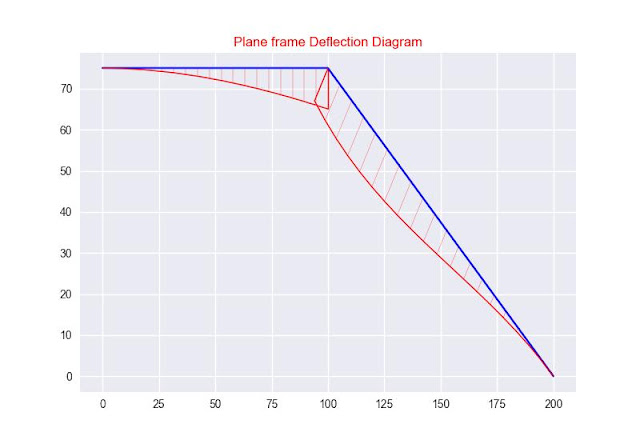
Plane Frame Analysis Using Python

 

Plane Frame for Analysis

Input Data from Textbook

#Plane Frame Analysis Program By Engr. I. Opoli

import numpy as np

import matplotlib.pyplot as plt

plt.style.use('seaborn')

np.set_printoptions(suppress=True,precision=3)

#Input Data

#Node coordinates

Node=np.array([[100,75],[0,75],[200,0]])

#Member connectivity

Conn=np.array([[1,0,10000,1000,10],[0,2,10000,1000,10]])

#Boundary condition

BC=np.array([[1,1,1,1],[2,1,1,1]])

#Joint loads

EJLD=np.array([[0,0,-10,-1000]])

#Member point loads

PLD=np.array([[1,-20,62.5,2]])

#Member UDLs

UDL=np.array([[0,-0.24,2]])

Input Data from Program

[[  1000.      0.      0.  -1000.      0.      0.]

 [     0.    120.   6000.      0.   -120.   6000.]

 [     0.   6000. 400000.      0.  -6000. 200000.]

 [ -1000.      0.      0.   1000.      0.      0.]

 [     0.   -120.  -6000.      0.    120.  -6000.]

 [     0.   6000. 200000.      0.  -6000. 400000.]]

Local Stiffness Matrix for Member 1

[[   800.        0.        0.     -800.        0.        0.  ]

 [     0.       61.44   3840.        0.      -61.44   3840.  ]

 [     0.     3840.   320000.        0.    -3840.   160000.  ]

 [  -800.        0.        0.      800.        0.        0.  ]

 [     0.      -61.44  -3840.        0.       61.44  -3840.  ]

 [     0.     3840.   160000.        0.    -3840.   320000.  ]]

Local Stiffness Matrix for Member 2

[[  1000.      0.      0.  -1000.      0.      0.]

 [     0.    120.   6000.      0.   -120.   6000.]

 [     0.   6000. 400000.      0.  -6000. 200000.]

 [ -1000.      0.      0.   1000.      0.      0.]

 [     0.   -120.  -6000.      0.    120.  -6000.]

 [     0.   6000. 200000.      0.  -6000. 400000.]]

Global Stiffness Matrix for Member 1

[[   534.118   -354.509   2304.      -534.118    354.509   2304.   ]

 [  -354.509    327.322   3072.       354.509   -327.322   3072.   ]

 [  2304.      3072.    320000.     -2304.     -3072.    160000.   ]

 [  -534.118    354.509  -2304.       534.118   -354.509  -2304.   ]

 [   354.509   -327.322  -3072.      -354.509    327.322  -3072.   ]

 [  2304.      3072.    160000.     -2304.     -3072.    320000.   ]]

Global Stiffness Matrix for Member 2

[[  1534.118   -354.509   2304.     -1000.         0.         0.  -534.118    354.509   2304.   ]

 [  -354.509    447.322  -2928.         0.      -120.     -6000.   354.509   -327.322   3072.   ]

 [  2304.     -2928.    720000.         0.      6000.    200000.  -2304.     -3072.    160000.   ]

 [ -1000.         0.         0.      1000.         0.         0.     0.         0.         0.   ]

 [     0.      -120.      6000.         0.       120.      6000.     0.         0.         0.   ]

 [     0.     -6000.    200000.         0.      6000.    400000.     0.         0.         0.   ]

 [  -534.118    354.509  -2304.         0.         0.         0.   534.118   -354.509  -2304.   ]

 [   354.509   -327.322  -3072.         0.         0.         0.  -354.509    327.322  -3072.   ]

 [  2304.      3072.    160000.         0.         0.         0. -2304.     -3072.    320000.   ]]

Global Stiffness Matrix for the Structure

[[-0.02 ]

 [-0.099]

 [-0.002]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]]

Computed Nodal deflection for the structure

[[  20.261]

 [  13.138]

 [ 436.648]

 [ -20.261]

 [  10.862]

 [-322.865]]

Computed Member End forced for member 1

[[  28.726]

 [  -4.533]

 [-677.135]

 [ -40.726]

 [  20.533]

 [-889.525]]

Computed Member End forced for member 2

Continuous Beam Analysis using Three Moment Theorem

 

Input Data

Textbook Values Moments

Textbook Values Shear Forces

Analysis Results

Reinforced Concrete Helical Staircase Analysis

 Input Data

Preliminary Calculations

Analysis Output

Continuous Beam Analysis using Mathcad

 

Continuous Beam Analysis Problem

Continuous Beam Input Data

Solution Step 1

Member Stiffness Matrices

Global Stiffness Matrrix

Members Diplacements

Member End Forces

Textbook Values

Truss Analysis Using Python Code Example 2

 #Node coordinates

Node=np.array([[0,0],[3,0],[6,0],[4.5,3],[1.5,3]])

#Member connectivity

Conn=np.array([[0,1],[1,2],[0,4],[4,1],[1,3],[3,2],[4,3]])

#Boundary condition

BC=np.array([[0,1,1],[2,1,1]])

#Joint loads

ELD=np.array([[4,0,-50],[3,0,-50]])

E=210000000

A = 0.0001

Input Data

[[ 7000.     0. -7000.    -0.]

 [    0.     0.    -0.    -0.]

 [-7000.    -0.  7000.     0.]

 [   -0.    -0.     0.     0.]]

Stiffness Matrix for member 1

[[ 7000.     0. -7000.    -0.]

 [    0.     0.    -0.    -0.]

 [-7000.    -0.  7000.     0.]

 [   -0.    -0.     0.     0.]]

Stiffness Matrix for member 2

[[ 1252.1980674  2504.3961348 -1252.1980674 -2504.3961348]

 [ 2504.3961348  5008.7922696 -2504.3961348 -5008.7922696]

 [-1252.1980674 -2504.3961348  1252.1980674  2504.3961348]

 [-2504.3961348 -5008.7922696  2504.3961348  5008.7922696]]

Stiffness Matrix for member 3

[[ 1252.1980674 -2504.3961348 -1252.1980674  2504.3961348]

 [-2504.3961348  5008.7922696  2504.3961348 -5008.7922696]

 [-1252.1980674  2504.3961348  1252.1980674 -2504.3961348]

 [ 2504.3961348 -5008.7922696 -2504.3961348  5008.7922696]]

Stiffness Matrix for member 4

[[ 1252.1980674  2504.3961348 -1252.1980674 -2504.3961348]

 [ 2504.3961348  5008.7922696 -2504.3961348 -5008.7922696]

 [-1252.1980674 -2504.3961348  1252.1980674  2504.3961348]

 [-2504.3961348 -5008.7922696  2504.3961348  5008.7922696]]

Stiffness Matrix for member 5

[[ 1252.1980674 -2504.3961348 -1252.1980674  2504.3961348]

 [-2504.3961348  5008.7922696  2504.3961348 -5008.7922696]

 [-1252.1980674  2504.3961348  1252.1980674 -2504.3961348]

 [ 2504.3961348 -5008.7922696 -2504.3961348  5008.7922696]]

Stiffness Matrix for member 6

[[ 7000.     0. -7000.    -0.]

 [    0.     0.    -0.    -0.]

 [-7000.    -0.  7000.     0.]

 [   -0.    -0.     0.     0.]]

Stiffness Matrix for member 7

[[ 8252.1980674  2504.3961348 -7000.            0.            0.

      0.            0.            0.        -1252.1980674 -2504.3961348]

 [ 2504.3961348  5008.7922696     0.            0.            0.

      0.            0.            0.        -2504.3961348 -5008.7922696]

 [-7000.            0.        16504.3961348     0.        -7000.

      0.        -1252.1980674 -2504.3961348 -1252.1980674  2504.3961348]

 [    0.            0.            0.        10017.5845392     0.

      0.        -2504.3961348 -5008.7922696  2504.3961348 -5008.7922696]

 [    0.            0.        -7000.            0.         8252.1980674

  -2504.3961348 -1252.1980674  2504.3961348     0.            0.       ]

 [    0.            0.            0.            0.        -2504.3961348

   5008.7922696  2504.3961348 -5008.7922696     0.            0.       ]

 [    0.            0.        -1252.1980674 -2504.3961348 -1252.1980674

   2504.3961348  9504.3961348     0.        -7000.            0.       ]

 [    0.            0.        -2504.3961348 -5008.7922696  2504.3961348

  -5008.7922696     0.        10017.5845392     0.            0.       ]

 [-1252.1980674 -2504.3961348 -1252.1980674  2504.3961348     0.

      0.        -7000.            0.         9504.3961348     0.       ]

 [-2504.3961348 -5008.7922696  2504.3961348 -5008.7922696     0.

      0.            0.            0.            0.        10017.5845392]]

Global Stiffness Matrix for the Structure

0     -0.0

1     0.0

2     -55.902

3     0.0

4     0.0

5 -    55.902

6     -25.0

Member forces for the Structure

Node No X-react Y-react

======= ======= =======

0     25.0     50.0

2     -25.0     50.0

Support Reactions for the Structure

Original and Deflected Shape of the Structure

Member forces for the Structure

Truss Analysis Using Python Code

Input Data

 #Node coordinates

Node=np.array([[0,0],[180,0],[180,240],[0,240]])

#Member connectivity

Conn=np.array([[0,2],[1,2],[3,2]])

#Boundary condition

BC=np.array([[0,1,1],[1,1,1],[3,1,1]])

#Joint loads

ELD=np.array([[2,50,-86.6]])

E=29000

A = 9

[[ 313.2  417.6 -313.2 -417.6]

 [ 417.6  556.8 -417.6 -556.8]

 [-313.2 -417.6  313.2  417.6]

 [-417.6 -556.8  417.6  556.8]]

Stiffness Matrix for Member 1

[[    0.      0.     -0.     -0. ]

 [    0.   1087.5    -0.  -1087.5]

 [   -0.     -0.      0.      0. ]

 [   -0.  -1087.5     0.   1087.5]]

Stiffness Matrix for Member 2

[[ 1450.     0. -1450.    -0.]

 [    0.     0.    -0.    -0.]

 [-1450.    -0.  1450.     0.]

 [   -0.    -0.     0.     0.]]

Stiffness Matrix for Member 3

[[  313.2   417.6     0.      0.   -313.2  -417.6     0.      0. ]

 [  417.6   556.8     0.      0.   -417.6  -556.8     0.      0. ]

 [    0.      0.      0.      0.      0.      0.      0.      0. ]

 [    0.      0.      0.   1087.5     0.  -1087.5     0.      0. ]

 [ -313.2  -417.6     0.      0.   1763.2   417.6 -1450.      0. ]

 [ -417.6  -556.8     0.  -1087.5   417.6  1644.3     0.      0. ]

 [    0.      0.      0.      0.  -1450.      0.   1450.      0. ]

 [    0.      0.      0.      0.      0.      0.      0.      0. ]]

Global Stiffness Matrix for the Structure

0 -21.657

1 -69.274

2 62.994

Computed forces for the Members

Node No X-react Y-react

======= ======= =======

Node No X-react Y-react

======= ======= =======

0     12.994     17.326

1             0.0     69.274

3         -62.994     0.0

Computed Reactions at the Nodes

Original and Deflected Truss Shape

Members Forces Diagram for the Structure

Structural Analysis of Plane Truss using Mathcad

 

Input data

Input data cont'd

Input data 2 cont'd

Truss diagram

Member forces

Truss original and deflected shape

Truss support reactions