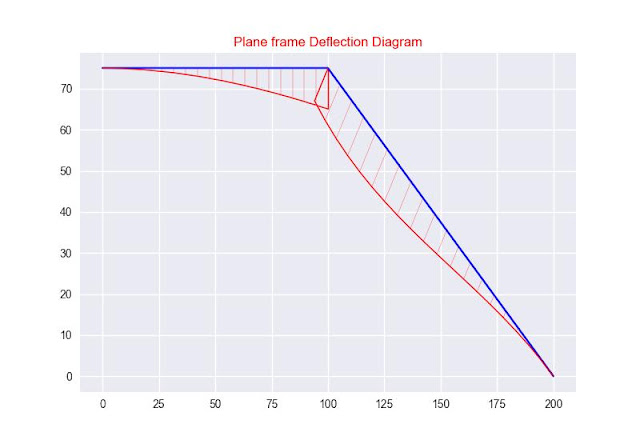
Plane Frame Analysis Using Python

 

Plane Frame for Analysis

Input Data from Textbook

#Plane Frame Analysis Program By Engr. I. Opoli

import numpy as np

import matplotlib.pyplot as plt

plt.style.use('seaborn')

np.set_printoptions(suppress=True,precision=3)

#Input Data

#Node coordinates

Node=np.array([[100,75],[0,75],[200,0]])

#Member connectivity

Conn=np.array([[1,0,10000,1000,10],[0,2,10000,1000,10]])

#Boundary condition

BC=np.array([[1,1,1,1],[2,1,1,1]])

#Joint loads

EJLD=np.array([[0,0,-10,-1000]])

#Member point loads

PLD=np.array([[1,-20,62.5,2]])

#Member UDLs

UDL=np.array([[0,-0.24,2]])

Input Data from Program

[[  1000.      0.      0.  -1000.      0.      0.]

 [     0.    120.   6000.      0.   -120.   6000.]

 [     0.   6000. 400000.      0.  -6000. 200000.]

 [ -1000.      0.      0.   1000.      0.      0.]

 [     0.   -120.  -6000.      0.    120.  -6000.]

 [     0.   6000. 200000.      0.  -6000. 400000.]]

Local Stiffness Matrix for Member 1

[[   800.        0.        0.     -800.        0.        0.  ]

 [     0.       61.44   3840.        0.      -61.44   3840.  ]

 [     0.     3840.   320000.        0.    -3840.   160000.  ]

 [  -800.        0.        0.      800.        0.        0.  ]

 [     0.      -61.44  -3840.        0.       61.44  -3840.  ]

 [     0.     3840.   160000.        0.    -3840.   320000.  ]]

Local Stiffness Matrix for Member 2

[[  1000.      0.      0.  -1000.      0.      0.]

 [     0.    120.   6000.      0.   -120.   6000.]

 [     0.   6000. 400000.      0.  -6000. 200000.]

 [ -1000.      0.      0.   1000.      0.      0.]

 [     0.   -120.  -6000.      0.    120.  -6000.]

 [     0.   6000. 200000.      0.  -6000. 400000.]]

Global Stiffness Matrix for Member 1

[[   534.118   -354.509   2304.      -534.118    354.509   2304.   ]

 [  -354.509    327.322   3072.       354.509   -327.322   3072.   ]

 [  2304.      3072.    320000.     -2304.     -3072.    160000.   ]

 [  -534.118    354.509  -2304.       534.118   -354.509  -2304.   ]

 [   354.509   -327.322  -3072.      -354.509    327.322  -3072.   ]

 [  2304.      3072.    160000.     -2304.     -3072.    320000.   ]]

Global Stiffness Matrix for Member 2

[[  1534.118   -354.509   2304.     -1000.         0.         0.  -534.118    354.509   2304.   ]

 [  -354.509    447.322  -2928.         0.      -120.     -6000.   354.509   -327.322   3072.   ]

 [  2304.     -2928.    720000.         0.      6000.    200000.  -2304.     -3072.    160000.   ]

 [ -1000.         0.         0.      1000.         0.         0.     0.         0.         0.   ]

 [     0.      -120.      6000.         0.       120.      6000.     0.         0.         0.   ]

 [     0.     -6000.    200000.         0.      6000.    400000.     0.         0.         0.   ]

 [  -534.118    354.509  -2304.         0.         0.         0.   534.118   -354.509  -2304.   ]

 [   354.509   -327.322  -3072.         0.         0.         0.  -354.509    327.322  -3072.   ]

 [  2304.      3072.    160000.         0.         0.         0. -2304.     -3072.    320000.   ]]

Global Stiffness Matrix for the Structure

[[-0.02 ]

 [-0.099]

 [-0.002]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]

 [ 0.   ]]

Computed Nodal deflection for the structure

[[  20.261]

 [  13.138]

 [ 436.648]

 [ -20.261]

 [  10.862]

 [-322.865]]

Computed Member End forced for member 1

[[  28.726]

 [  -4.533]

 [-677.135]

 [ -40.726]

 [  20.533]

 [-889.525]]

Computed Member End forced for member 2

Continuous Beam Analysis using Three Moment Theorem

 

Input Data

Textbook Values Moments

Textbook Values Shear Forces

Analysis Results

Reinforced Concrete Helical Staircase Analysis

 Input Data

Preliminary Calculations

Analysis Output

Continuous Beam Analysis using Mathcad

 

Continuous Beam Analysis Problem

Continuous Beam Input Data

Solution Step 1

Member Stiffness Matrices

Global Stiffness Matrrix

Members Diplacements

Member End Forces

Textbook Values